Home | Algorithms | Architecture | Construction of Conflictgraph
Description of the algorithms
For modeling the intersection in the backend with its traffic lanes and pedestrian crossings we used a conflict graph. Each node represents a lane on the intersection. If the cars of two lanes can´t drive at the same time, because their lanes cross each other, the conflict graph has an edge between this to nodes.
By coloring the graph it is possible to retrieve all nodes which can drive at the same time. With Basic Greedy and Welsh Powell we selected two algorithms to color the conflict graph. Bron Kerbosch is using cliques to retrieve the traffic light phases from a compatibility graph.
The following sections describe the algorithms more detailed:
Basic Greedy
The Basic Greedy algorithm is a very easy algorithm for coloring a graph. The solution heavily depends on the order of the vertices. Furthermore Basic Greedy does not deliver a colored graph with minimum number of colors.
1. Color first vertex with first color.
2. Do following for remaining V-1 vertices.
2.1 Consider the currently picked vertex and color it with the
lowest numbered color that has not been used on any previously
colored vertices adjacent to it. If all previously used colors
appear on vertices adjacent to v, assign a new color to it.
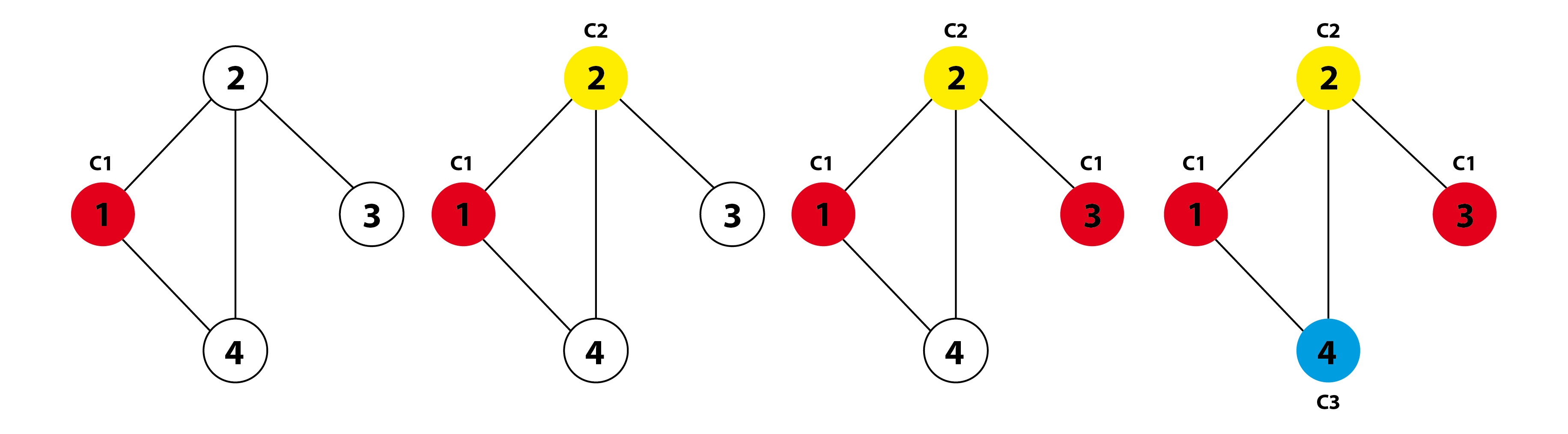
Welsh Powell
This algorithm is simular to the Basic Greedy algorithm. But the welsh powell algorithm has two speciality:
- first order the nodes descending by count of edges
- then find nodes with no conflict and color this in same color
1. Order the nodes by conflict graph descending by count of edges
2. Color first vertex (most edges) with first color.
3. Pass through all other nodes. When this node has no conflict with other nodes with same color, color this node in same color
4. Repeat this with all other nodes pending all nodes have colors
 source: https://www.youtube.com/watch?v=CQIW2mLfG04
source: https://www.youtube.com/watch?v=CQIW2mLfG04
Bron Kerbosch
Despite of the other two algorithms, the Bron-Kerbosch Algorithm relies on a compatibility graph rather than a conflict graph. It will find all the biggest groups of lanes that are compatible to each other.
It does this by using two principles:
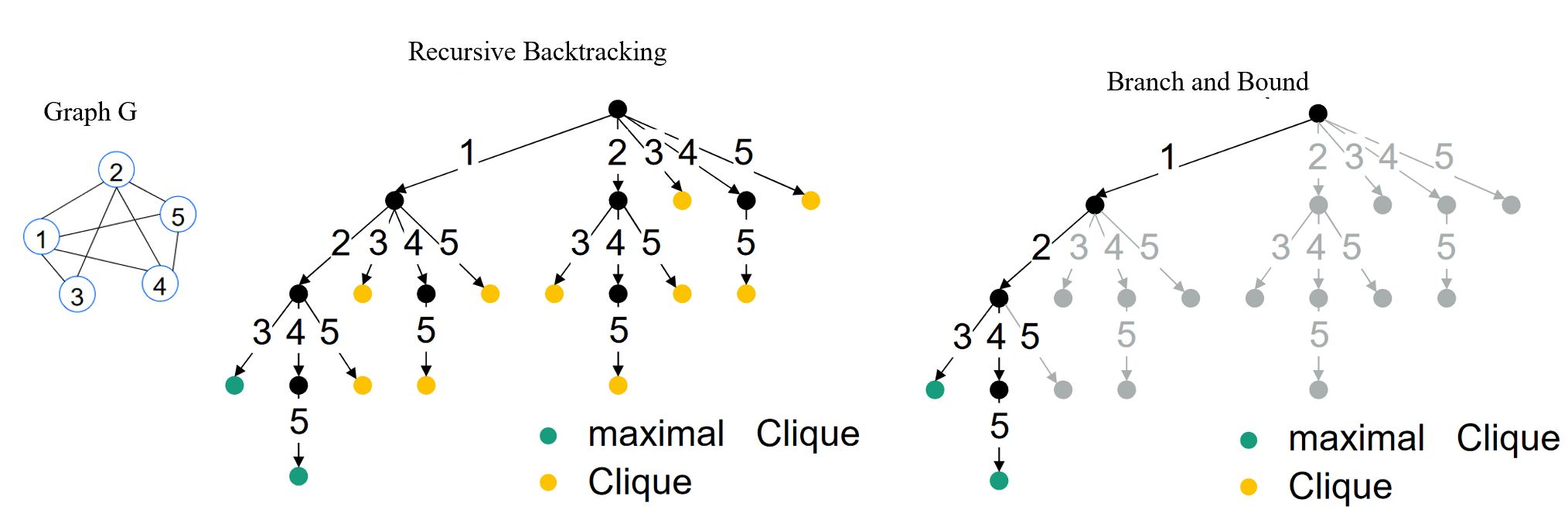
The recursive backtracking procedure- a efficient recursive search algorithm to go through a graph
- it does not search for permutations of cliques that have already been found
The branch- and bound method- if a subtree will not lead to a maximal clique, the search on this branch is to be aborted Example:
Source: http://kontext.fraunhofer.de/haenelt/kurs/folien/Haenelt_Clique.pdf
Bron_Kerbosch(list next_possible_expansions, list<node> current_list, list already_tested)
if current_list.isempty() and already_tested.isempty():
next_possible_expansion is a maximal clique
else
for all nodes v in clique:
NEW_next_possible_expansions = next_possible_expansion.append(v)
NEW_current_list = current_list .getNeighbors(v)
NEW_already_tested = already_tested .getNeighbors(v)
Bron_Kerbosch(NEW_next_possible_expansions, NEW_current_list, NEW_already_tested)
current_list = current_list.remove(v)
already_tested = already_tested.append(v)
In our own version we tackled a issue that was making the Bron Kerbosch Algorithm in the original form unusable for our specific Problem: The Bron Kerbosch gives all the biggest cliques that the graph has to offer. As a result there a many lanes that appear multiple times over in the cliques that are given by the Bron Kerbosch Algorithm. As we did not want lanes to appear multiple times, we essentially cut out all the doubles and triples afterwards and all the cliques that are unnecessary to the final solution.